What is QBism?
Quantum physics works. But why?
Why does this theory, which is surely one of the jewels of modern physics, deal with probabilities rather than certainties? Why is the calculation of those probabilities mediated by complex numbers, rather than any of the other entities that mathematicians have devised? How is it that we can have so many “pictures” of the same theory—that we can use, for example, the matrices of Heisenberg, the waves of Schrödinger or the path integrals of Dirac and Feynman, all these schemes being ultimately equivalent, yet convenient for approaching different problems? Are the representations we know of today exhaustive? What portions of the mathematical formalism are human convention, mere frozen historical accidents, and which portions truly reflect characteristics of the natural world that were here before we were and that would endure in our absence? Is there an ordering on the set of theorems derived within quantum theory other than historical happenstance, a principled way of separating the results which were merely unexpected from those that are truly enigmatic? Why are the most striking phenomena—the violation of Bell inequalities, the possibility of quantum computation—hidden deep within the formalism, buried below several chapters of derivations and hardly apparent at all from the way the theory is first introduced? Is there a better way to do the job: Can we start with a crisp statement of exactly how natural randomness resists explanation in terms of intrinsic hidden variables, and from that basic principle derive all the complex amplitudes, all the unitary matrices, all the Kraus operators and completely-positive trace-preserving maps?
Most philosophically: Why do concepts like “observer” and “measurement” play such a prominent role in efforts to give the mathematics of quantum theory a physical meaning? Ought we try to excise them, or is the situation more like how the pioneering experimentalist Anton Zeilinger put it: Measurement is an essential part of doing science, and so it is only natural that developing a theory of measurement would eventually be necessary for scientific progress. Perhaps we could ameliorate the conceptual difficulties of quantum physics if we admitted to ourselves that at least some of the mathematical entities in the theory are encodings of information. For example, from this perspective, the notorious “collapse of the wavefunction” becomes not so shocking after all. The wavefunction you write down for a physical system is your catalogue of expectations about that system and what it might do when you interact with it. And if a mathematical object is really a catalogue of what you find plausible about the potential behavior of a physical system, or of what you expect to be feasible to achieve using that system, then it is only natural that that mathematical entity change radically or even discontinuously at times. Your expectations for what might happen to you when you perform an action on a system certainly can change when you actually go and carry out that action!
Just as probability theory made quantitative the notion of expectation, and information theory gave exact expression to ideas of communication, perhaps quantum theory is ultimately a formal theory of action and consequence, of agency and creativity.
This is the viewpoint of QBism, an interpretation of quantum mechanics due to Christopher Fuchs and Rüdiger Schack, and promoted more recently by David Mermin and Theodor Hänsch (Nobel Prize in Physics, 2005). QBism draws upon the traditions of Pauli, Wheeler, Peres and others, striving to make a consistent whole out of their varied insights. To a QBist, quantum theory is a “hero's handbook”: It is a tool, expressed in the language of probability, for keeping one's expectations consistent and making decisions in a natural world that has a certain character—the quantum character. As Mermin writes, it is in some ways an interpretation for physicists who don't like the business of “interpretation” very much. It means that the things physicists do with the theory day in and day out are “really all right after all,” but the price for knowing that one's actions are philosophically justified is to be more careful than physicists typically are about the meaning of probability.
Providing a meaning for the mathematics of quantum theory is one thing, and depending on one's own temperament, that may be enough. But another student might, with equal validity, feel discontented: If these philosophical seeds are so potent, should they not grow technical fruit? Better yet, if the germ of quantum physics really does lie within QBism, then ought there not to be a way to start from physical principles, manifestly QBist in character, and rederive the apparatus of quantum theory?
Over the past several years, the project of reconstructing quantum mechanics has been taken up, not just by QBists and sympathizers, but by others as well, though the theme of quantum states as information runs through much of the discussion. These efforts begin with a set of axioms, typically expressed in operationalist terms as statements about what kinds of laboratory procedures are possible, and rederive quantum theory from that starting point. Mathematically, these derivations are successful; however, they share the common feature that they make quantum theory as “benignly humdrum” as possible. The remarkable and enigmatic phenomena seen within quantum physics are no closer to the surface than they were in the standard presentation of the formalism. So, we have encouraging results to build upon, but there is work yet to be done.
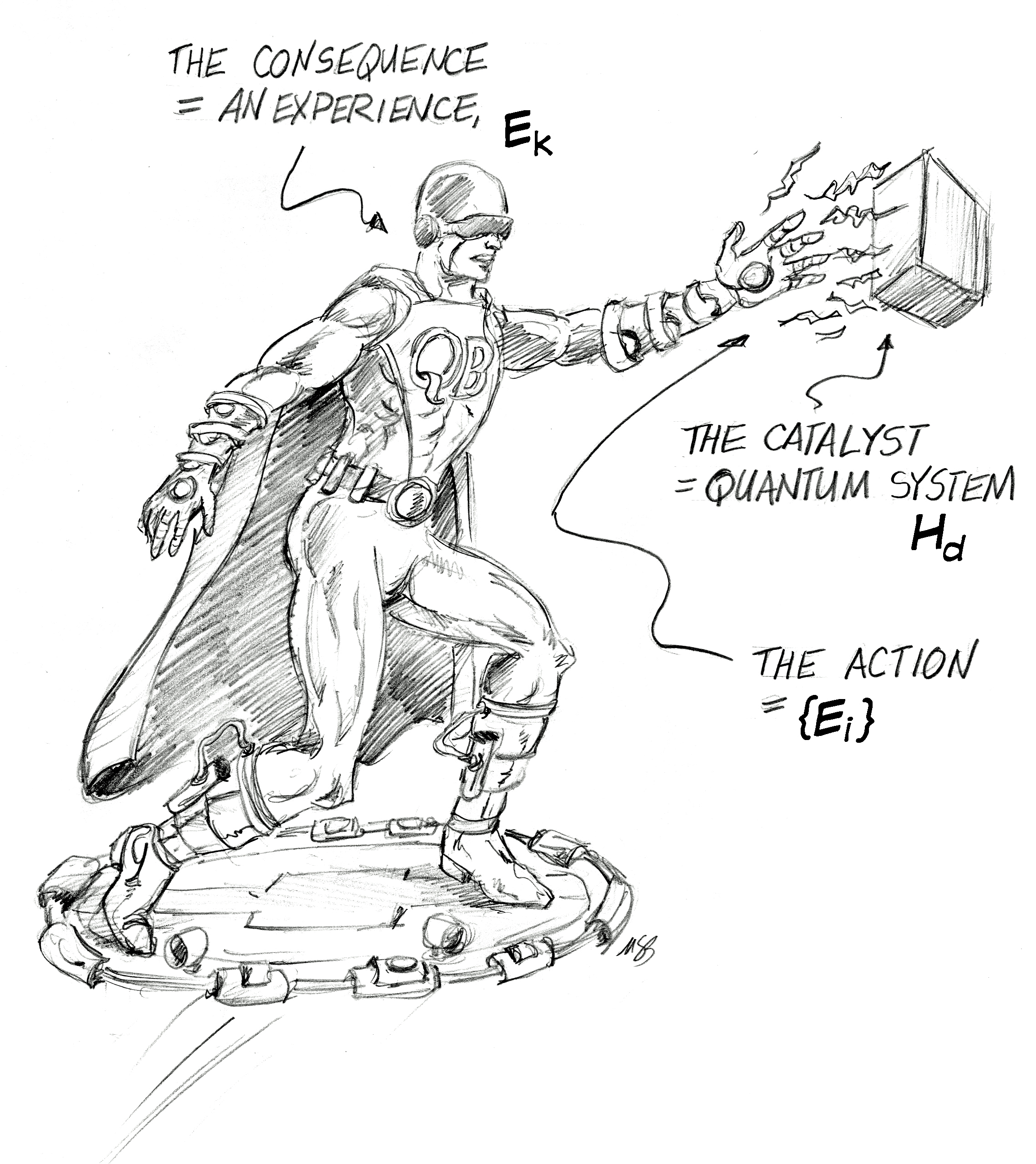
|
| Captain QBism prepares to take action—that is, perform a quantum measurement—using quantum theory to manage his expectations about what that action might bring into being. For details of the mathematical notation, see arXiv:1612.07308. (Drawing courtesy Mark Staff Brandl.) |
The technical centerpiece of our reconstruction program is a special type of measurement procedure, known as a Symmetric Informationally Complete quantum measurement, or a SIC. Geometrically speaking, a SIC is a set of d2 rays drawn from the origin of a d-dimensional complex vector space, such that any two rays meet at the same angle. By the rules of quantum mechanics, this corresponds to a measurement that one can perform on a d-level quantum system, with each ray standing for a possible outcome of the experiment. Moreover, this measurement is “informationally complete,” in that if one has a probability distribution for the d2 possible outcomes of the SIC experiment, one can compute the probability distribution over the outcomes of any other experiment that one can define in quantum theory. Like path integrals and Wigner functions before them, SICs provide a new “picture” of quantum physics. We are just beginning to see what calculations this new picture facilitates, but one idea that comes through clearly is that SICs help us quantify the deviation from classicality that quantum probabilities enable.
In quantum physics, probability distributions for different experiments that one can perform on the same system mesh together in a nonclassical way. SICs give us a novel quantitative expression of this fact. By taking this expression as a fundamental principle, we have found that we can go a long way towards rederiving quantum theory. This is encouraging: The enigma is buried no longer, but rather brought to the very starting point. However, the final step in our reconstruction requires an assumption that is stronger than we like, and indeed, stronger than we think is truly necessary.
Another difficulty is that we do not know for sure whether a SIC construction actually exists for every value of the dimension d. We have high-precision numerical solutions for every dimension up to 151, and several cases beyond that; also, exact solutions are known in many cases up to dimension 48. The common sentiment in the quantum information community is that at least one SIC does exist in every dimension. During the past two decades, many have worked on the SIC problem, and even though a general proof still eludes us, plenty of surprises have turned up along the way. For example, SICs have an unexpected connection to algebraic number theory, illuminating Hilbert's (as yet unsolved) twelfth problem from a remarkable new angle. Also, we have found that SICs relate to higher-dimensional sphere packing and ADE classification.
For more, see our Recommended Readings page.