Creating a Quantum Coherent State of the Relative Distance between Two Solitons in a Breather

We are exploring a possibility for a creation of a coherent quantum state of the macroscopic degrees of freedom of BEC solitons. In particular, we showed that in a quench from a single soliton to a breather (a bi-soliton), the relative coordinate of the two constituent daughter solitons is emerges cold and coherent, regardless of how hot the center of mass of the mother soliton was^[YMHOA17].

Creation of a breather in realistic conditions is optimized in^[GRDMOD18]. The quatum-fluctuation-induced spatial separation of the constituent solitons can be accelerated using repulsive barriers^[MMYODH19]. The underlying integrability can be shown to remain intact for a wide range of parameters^[DO15].

Interferometry with the Center-of-Mass of a Quantum Solitons

We are investigating the ways of protecting the center of mass state of single solitons: in particular, adding a lattice enforces an energy gap between the solitonic ground state and its excitations^[NGMMOA18]. We demonstrate numerically that for the same interferometer geometry, the absolute lower bound for a detectable angular velocity decreases N-fold when the individual atoms are lumped into a single soliton^[NGDPOAM19].

Scale Invariance and Quantum Anomalies

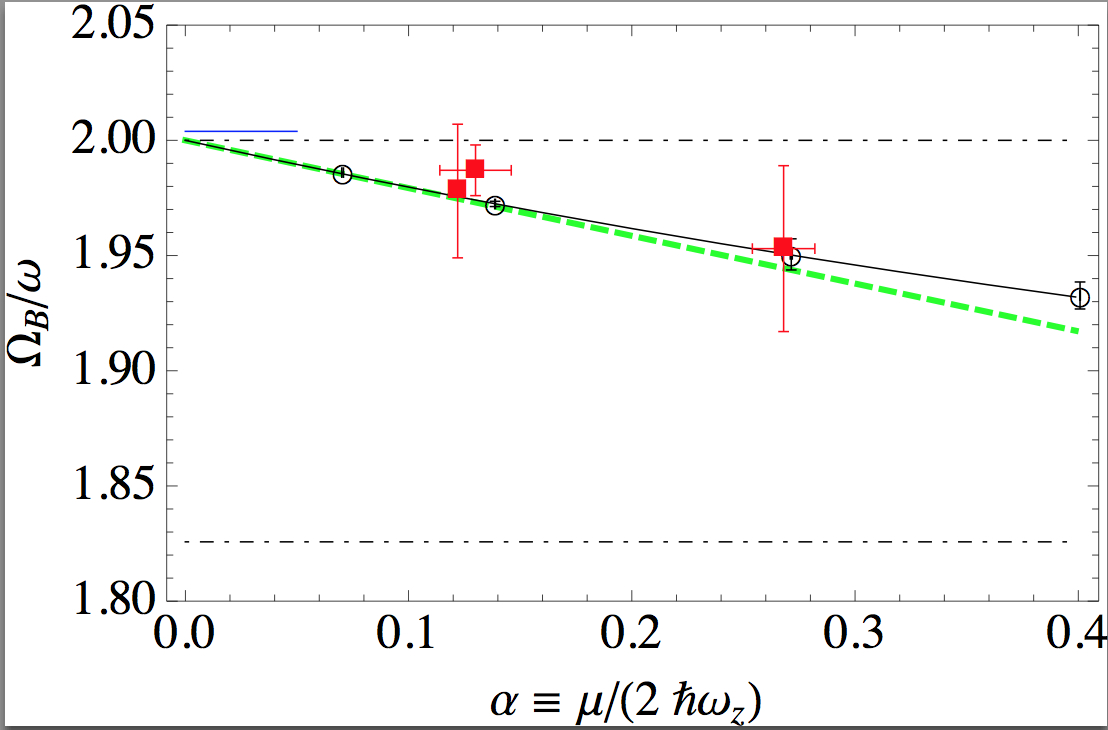
We are interested in the rare examples of systems with no length scales and in the consequences of weak breaking of this property. One of the most prominent properties of scale-free gases is the monochromaticity of the breathing excitations: their frequency is strictly fixed to be the double of the trapping frequency, for any amplitude. In the case of two-dimensional Bose gases, the departure from this law may occur due to quantum effects (the so-called quantum anomaly)^[OPL10], and due to the weak residual interaction with the third dimension^[MDL13] (see the results of our experimental-theoretical study on the left).

Similar results are obtained for one-dimensional p-wave-interacting fermions, and for bosons near the Tonks-Girardeau regime ^{[CDZO15] [ZAA14]}.

The quantum anomaly predicted in ^[OPL10] has been recently observed experimentally [Murthy et al, arXiv:1805.04734; Peppler et al, arXiv:1804.05102].

Integrable Many-Body Systems and Platonic Solids

Since the mid-70's, it has been believed that there exist only two types of reflection groups that can generate exact solutions to quantum N-body problems with short-range interactions: A_N-1 and C_N. These, respectively, allow one to solve the problem of an ensemble of atoms of identical masses on a ring, and in a box.

We show^[JO15], however, that the eigenenergies and eigenstates of a system consisting of four one-dimensional hard-core particles with masses 6m, 2m, m, and 3m in a hard-wall box can be found exactly using the Bethe ansatz based on the reflection group F₄. The latter is associated with the symmetries and tiling properties of an octacube : a Platonic solid unique to four dimensions, with no three-dimensional analogues. A particular section of the ground state wavefunction is shown on the left.

Recently, we extended the above method to non-crystallographic reflection groups, to the symmetries of the 3D and 4D icosahedra (H₃ and H₄) in particular^[SSJO16].

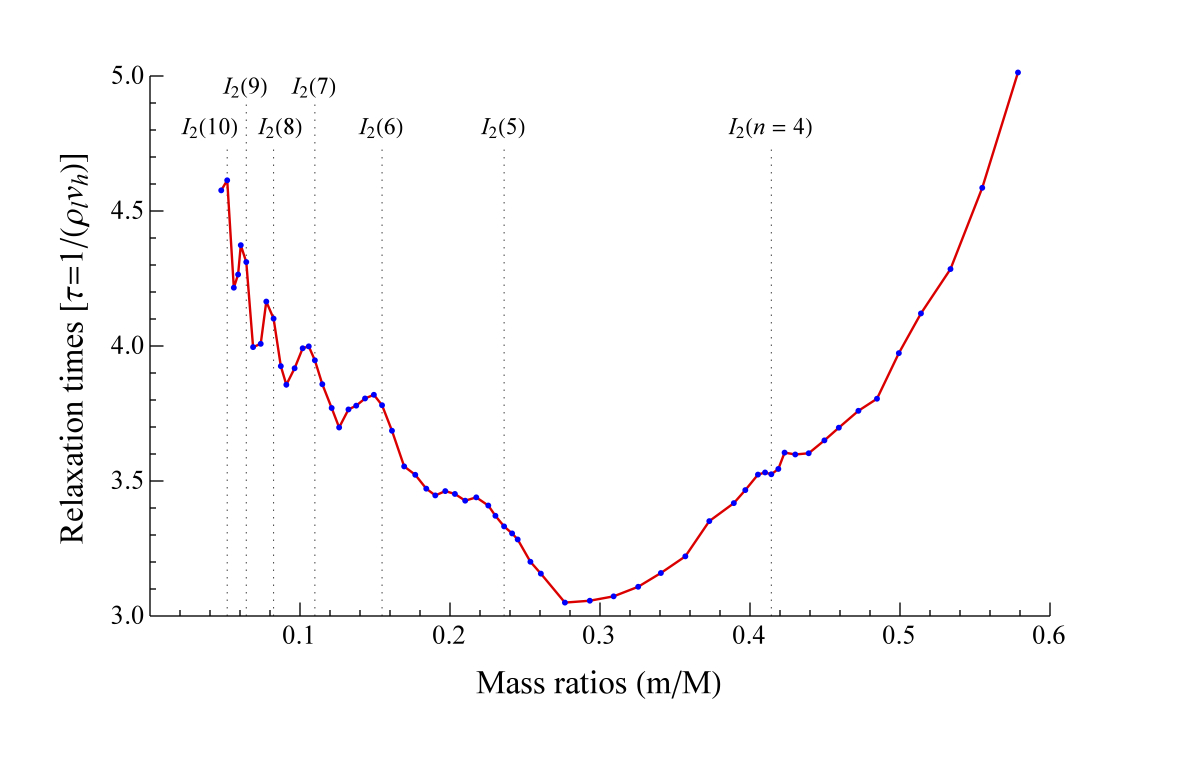
We invoke the reflection groups of regular polygons 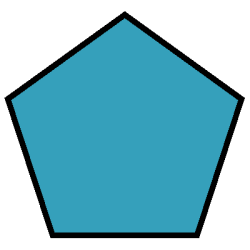, I₂(n), to predict and confim numerically^[HCO15] (see also ^[AGHJOA17]) the distinct peaks in the dependence of the relaxation time on the mass ratio in a one-dimensional mixture of atoms of two different masses, with hard-core interactions [figure to the right].

Harmonically trapped atoms lead to spherical billiards. Similarly to the relative motion of N particles on a line, integrability of N atoms in a harmonic potential is governed by the finite N-1-dimensional reflection groups; in particular, the integrable mass spectra are identical for these two models. We study explicitly the four-body integrability instances, given by the tetrahedral, cubic/octahedral, and dodecahedral/icosahedral symmetries, A₃, C₃, and H₃ respectively, and in the case of H₃, demonstrate numerically a transition from a Wigner-Dyson to Poisson statistics for an H₃ mass ratio set^[HODVJZ17].

Of a particular interest is the ability of integrable systems to stir the quantum evolution towards entangled states. We study this effect in the context of a so-called Galilean Cannon, in turn related to the symmetries of the N-dimensional tetrahedra, A_N. In an interferometric scheme we suggest^[OSDJ16], a light particle is beam-split and then, subsequently entangled with a heavy component of the system that never sees a beamsplitter. This scheme, if used as a sensor, shows an (N_atoms)^1/2 increase in sensitivity as compared to the conventional scheme, for the same total number of atoms N_atoms.

Other Bethe-Ansatz-based Projects

We study in detail a Calogero-Sutherland model with screening^[PBOC17]. We find that an introduction of a radius r screening (cut-off of interactions between two atoms when the latter are separated by more than r-1 other atoms) does not affect the integrability of the system, and, as in the un-screened case, the spectrum is controlled by the A_N-1 reflection group, for N atoms.

We revisit correlations in the Lieb-Liniger model (δ-interacting bosons on a ring) and find a connection between the local three-body correlation function and the forth derivative of the one-body correlator^[ODML17].

In the problem of scattering of a bosonic dimer on a barrier, we find that while the whole problem is not Bethe Ansatz integrable, it shares a part of its Hilbert space with an integrable problem associated with the C₂ reflection group^[GMO19]. As a result, the dimer dissociation becomes prohibited for spatially odd incident states. We suggest using this effect to effectuate a spatially compact readout off a chip-based atom interferometer.

We realized that under a stereographic projection, finite four-dimensional reflection groups induce three-dimensional finite groups of sphere inversions. This allows one to generate 19 3-parametric families of solvable electrostatic problems^[OSYDJ19].

Scattering without Reflection, QM-SUSY, and the Inverse Scattering Transform

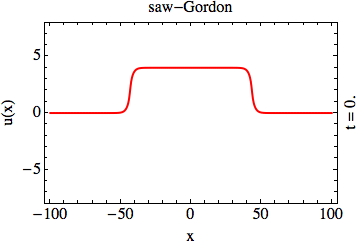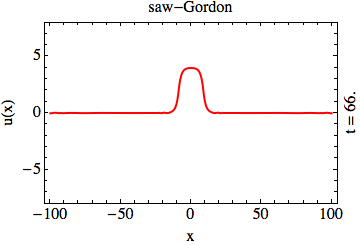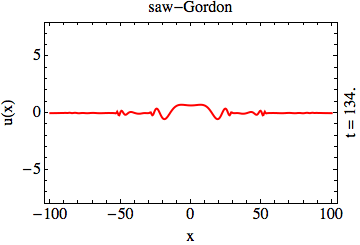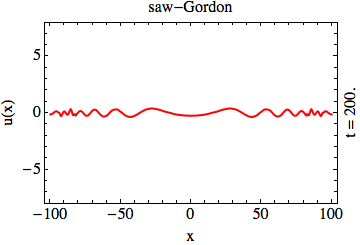
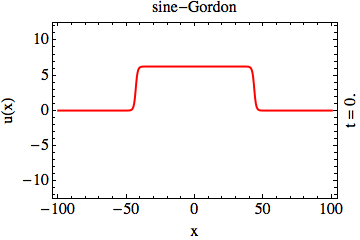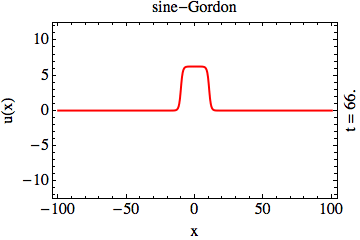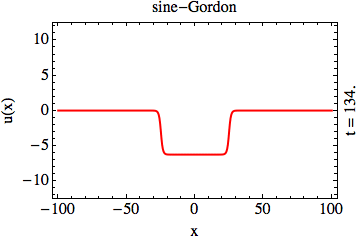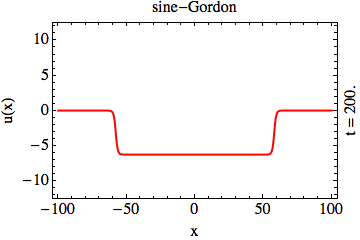
In the context of solitons in integrable partial differential equations, transparent potentials emerge in two unrelated instances: first, as the Lax operators (whose eigenvalues are the integrals of motion of the PDE in question); and second, as the Bogoliubov-de-Genes (BdG) Hamiltonians (emerging from the linearization of the PDE). Transparent potentials, Lax operators, and BdG Hamiltonians form an entagled web the structure of which is yet to be understood.

While the transparency of the solitonic Lax operators is well understood, the similar assertion about solitonic BdG Hamiltonians is far from obvious. To this end, we show that the transparency of the BdG Hamiltonian is in fact a necessary condition that ensures the mutual transparency of the solitons (the sine-Gordon animation, above); the appearance of the reflection of waves in the BdG problem leads to a mutual destruction of the solitary waves upon collision (the “saw”-Gordon animation, above) ^[KHO15].

The transparency of both the Lax and the BdG Liouvillians can be analyzed using the methods of the quantum-mechanical supersymmetry (QM-SUSY) ^{[KO11] [KHO15]}

We found that when one applies a nonintegrable perturbation to an integrable PDE, the notion of the “strength” of the perturbation depends dramatically on whether one works with the original equation or recasts the dynamics in Lax terms. For example, dramatic changes in the velocity of solitons can become small effects in the Lax formalism. We see this when we study the scattering of a two-soliton (a nonlinear superposition of two simple solitons that is itself an exact solution of the PDE) off a barrier. In the Lax context, the soliton velocity is a small real part of a complex number whose imaginary part, given by soliton's weight, is much larger in magnitude and, therefore, only negligibly changed in the process ^[DO15].

Two- and three-dimensional BEC solitons

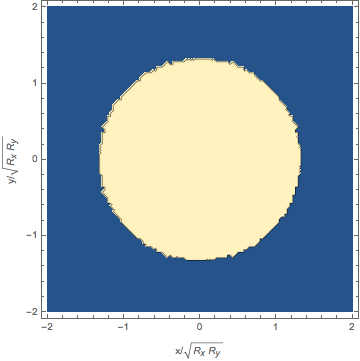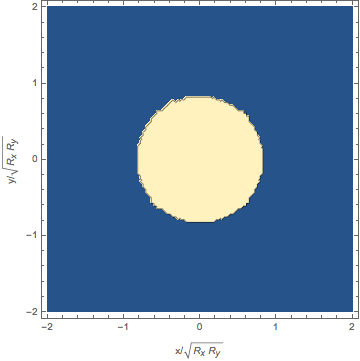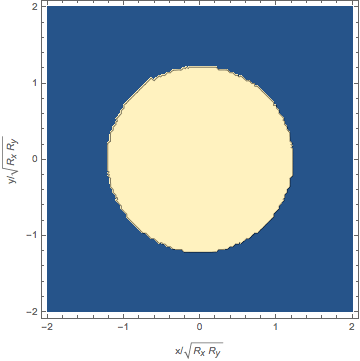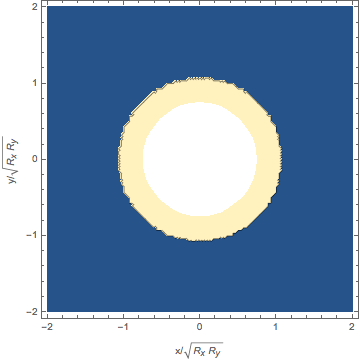
We addressed the question of stabilization of the three-dimensional bosonic solitary waves. To this end, we suggest altering the atomic disperion from quadratic to quartic using shaken optical lattice. We show that quartic dispersion is strong enough to support 3D solitary waves of arbitrary size and unlimited mobility ^[OCD15].

This reserch direction is devoted to the study of quantum nonequilibrium states and their applications in atomtronics. We began by suggesting a simple way of incorporating nontrivial conserved quantities in a thermodynamical description of a system ^[RDYuO07]. Next, we gave a straightforward numerical justification for the Eigenstate Thermalization Hypothesis, the cornerstone of the quantum nonequilibrium studies ^[RDO08]. The memory of the initial conditions in various quantum systems has been studied in ^{[OJRD12] [YuO11] [SAYuO10]}. 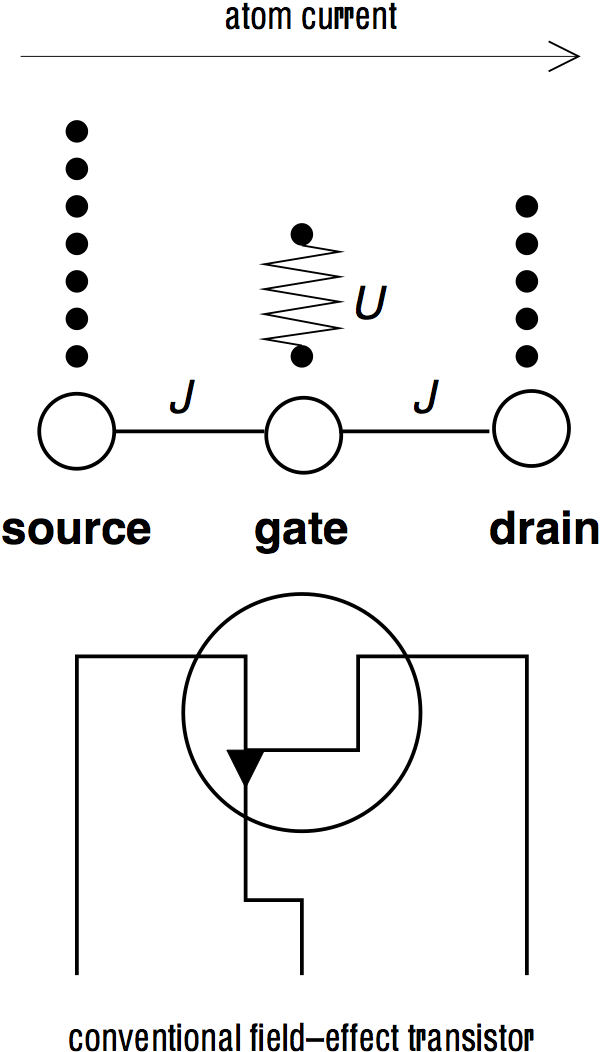The ultimate goal of this direction of research is to formulate a thermodynamical description that would universally apply to mesoscopic and/or near-integrable quantum systems ^{[Ols15] [SJD14]}. The atom transitor (right), is the primary object of interest ^[ZDO15].

Back-Of-The-Envelope Quantum Mechanics: With Extensions To Many-Body Systems And Integrable PDEs (World Scientific (2013))

A Contemporary Physics review on this book can be found here.

Errata.

"The quantum steampunker by Massachusetts Bay," by Nicole Yunger Halpern, Quantum Frontiers, October 27, 2019

Generalized Gibbs Ensemble, Quantum Steampunk, diode bridges, and all that.

"Pop Science," by Roger Highfield, New Scientist, 29 October 2011

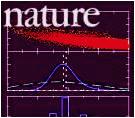
A popular report on various studies of explosions, both in science and in the arts. Our Nature study is presented as an example of research in the field of quantum explosions.

"Molecular surprise in one dimension," Physics World, June 9, 2005

A report on an experimental confirmation of the prediction of the existence of waveguide-confined molecules for both attractive and repulsive interactions between constituent atoms.

"Rhombic dodecahedron," Michel Serratrice, 2015

"Rhombic Dodecahedron," an artwork by Michel Serratrice, was directly inspired by our musings on octacubes. The rhombic dodecahedron in 3D and the octacube in 4D are members of a sequence of space-tiling d-dimensional solids obtained via the following procedure: a d-dimensional cube is split into pyramids, 2d of them, with its center as their common apex and its (d-1)-dimensional faces as their respective bases; the pyramids are then reflected about their bases, forming a new d-dimensional solid.